Calculating π with the Monte Carlo Simulation

When I was in university, I first learned about the Monte Carlo Simulation as way to calculate π (pi). The simple – yet genius – idea behind this concept just blew my mind. Calculating an infinite number like pi doesn't sound like fun for most people. Still, seeing the number getting more and more precise continues to amaze me. In order to refresh some old memories, I decided to implement an interactive simulation in React and TypeScript.

Let It Rain

Let me explain the idea behind the Monte Carlo Simulation with an analogy to rain. Take a sheet of paper and draw a unit square (whose sides have length 1) on it. Inside this unit square, draw a quarter circle with a radius of 1. It will look like this:

Now, let's imagine it is raining on this unit square with perfect randomness. The raindrops are going to be evenly distributed on the unit square. Some raindrops will lie inside the quarter circle (i.e. blue dots), and some will lie outside of it (i.e. red dots). Logically, a lot more raindrops will fall inside the quarter circle than outside of it. This is what it looks with 1000 raindrops:

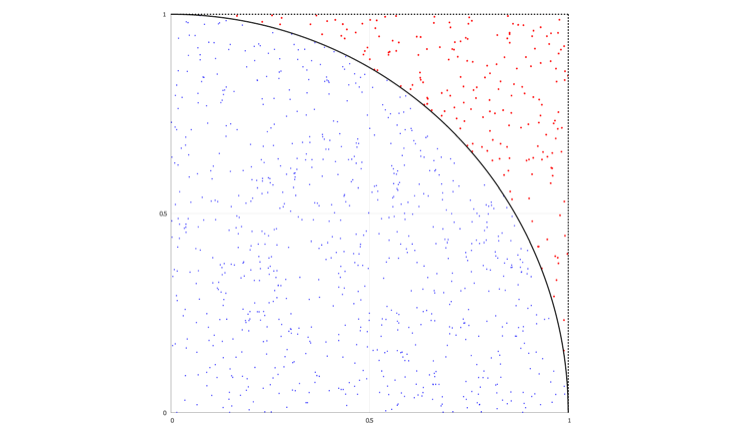
Interestingly, the fraction of raindrops inside the quarter circle over the total number of raindrops will constantly change as we generate more raindrops. This is due to the law of large numbers and the fact that we reach ever better distribution. Let's keep this fraction in mind as we're going to need it in the next step.

Give Me The Math

I'm going to briefly explain the underlying math principle. There are plenty of good articles on the Internet for more detailed information. The method is based on the mathematical formula for calculating the area of a unit circle (i.e. the one with radius 1):

We are going to cut the unit circle in four equal segments. The derived quarter circle (i.e. the blue area) still has a radius of 1 and its area is defined by the following formula:

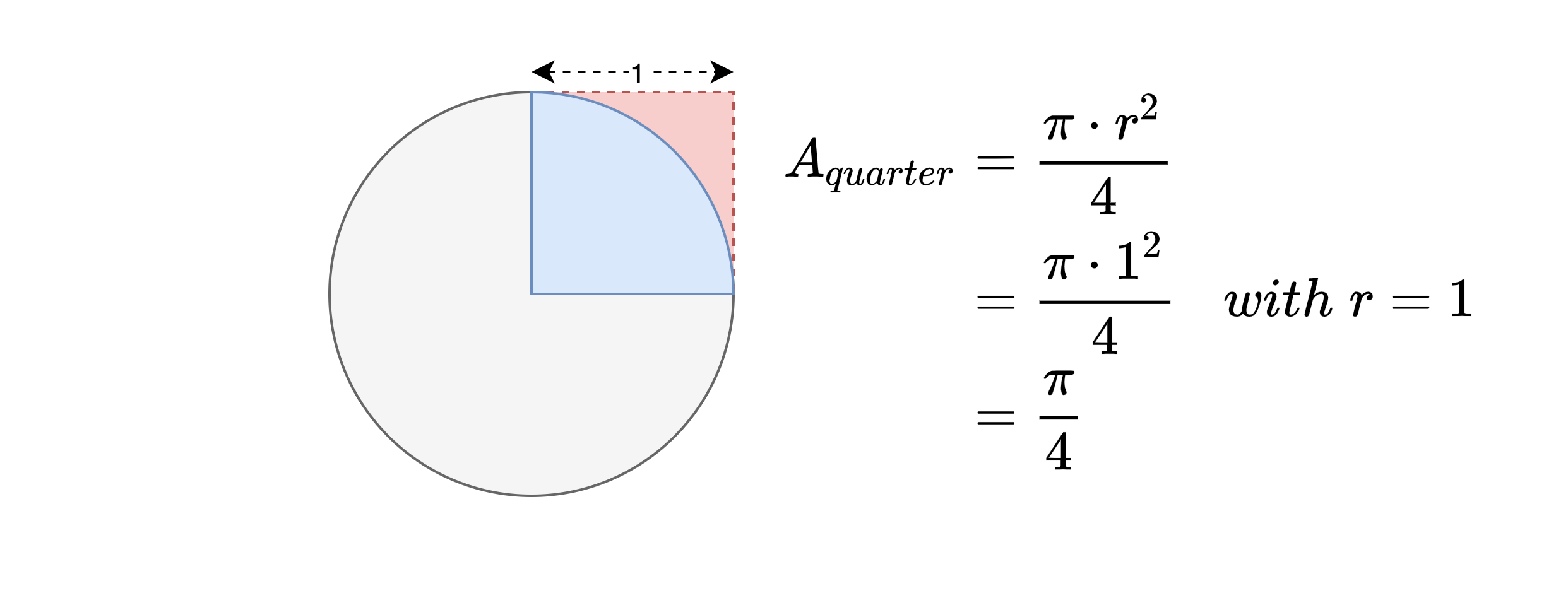
Now interestingly, the quarter circle fits perfectly well into a unit square (i.e. the red area) with an edge length of 1. We know that the unit square has an area of $1\times1$ and the quarter circle partly overlaps with this area as defined by the previous formula for $A_{quarter}$. We must assume the fraction to which it overlaps – and the way of doing that – is by generating random points within the unit square (e.g. we let it rain).

This fraction can be defined as $\frac{drops\;inside\;the\;quarter\;circle}{total\;number\;of\;drops\;generated}$ or abbreviated as $\frac{i}{t}$. From here, we can build an equation with a fraction of the quarter circle area over unit square area equal the fraction of the drops inside the quarter circle over the total number of drops. This equation must then be solved for π and leads us to the following equation:

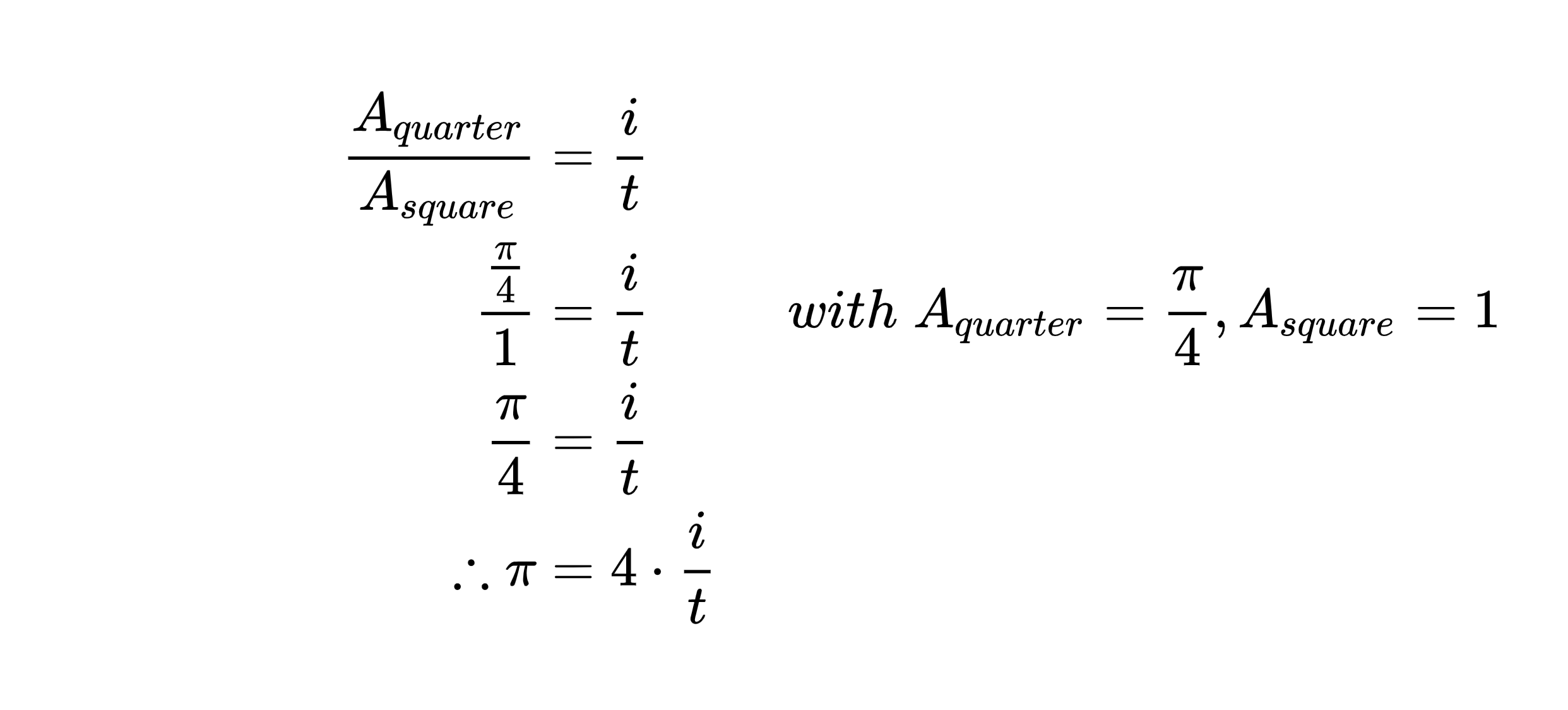
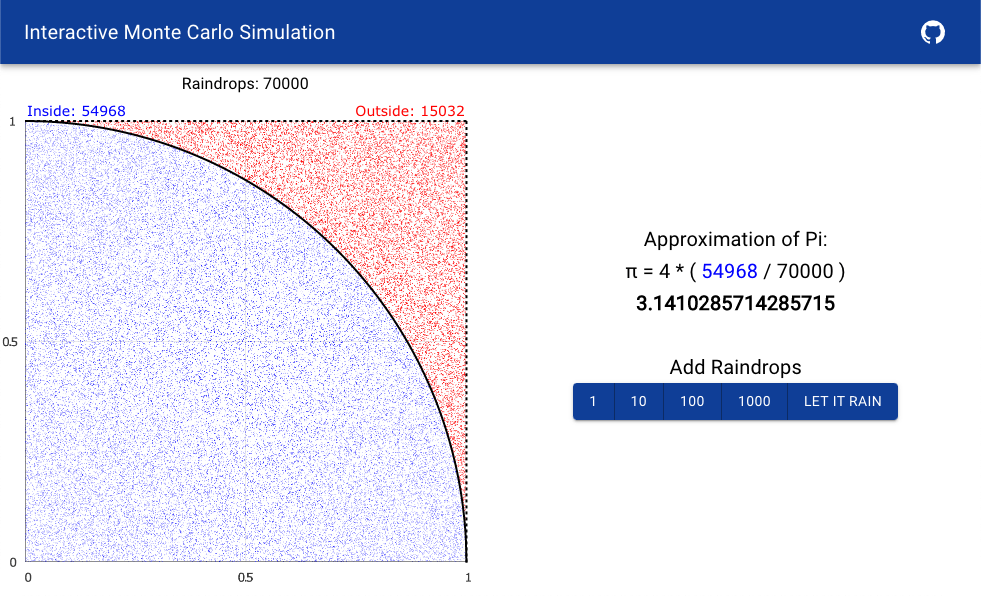
Interactive Simulation

I have implemented an interactive simulation in React and Typescript. The app uses Plotly.js to draw the unit square, the quarter circle and the raindrops. I have added a few buttons to randomly generate 1, 10, 100 or 1000 of raindrops. The raindrops are colored blue if they fall inside the quarter circle, otherwise they are colored red. There's also a special button labelled as Let It Rain to continuously generate raindrops as if it were raining. After each update, the approximate value of Pi is calculated again based on the newly generated raindrops. The more raindrops, the more accurate the value of Pi.

bookmark